Einfache Lineare Regression (Teil 1)

Vorhersagemodell für die Waldbrandgefahr in Deutschland

In diesem Teilmodul wird ein Vorhersagemodell entwickelt, das die Waldbrandgefahr in Deutschland einschätzt. Grundlage sind historische Satellitendaten, unter anderem zur Oberflächentemperatur, zur Niederschlagsmenge und zum Vegetationsindex. Zunächst wird ein einfaches lineares Regressionsmodell erstellt, das sich allein auf die Oberflächentemperatur stützt. Dabei werden grundlegende Konzepte des maschinellen Lernens vermittelt, insbesondere das Gradientenverfahren.

Autor:in

Zugehörigkeit

Sören Sparmann

Universität Paderborn

Veröffentlichungsdatum

14. September 2025

1 Waldbrände in Deutschland

Mit deutschlandweit 2397 Waldbränden ist 2022 ein deutlich überdurchschnittliches Waldbrandjahr im Vergleich zum mehrjährigen Mittel der Jahre 1993 bis 2021 (1.029 Waldbrände). Auch bezüglich der betroffenen Waldfläche ist das Jahr 2022 mit 3.058 Hektar - dies entspricht in etwa der Größe der Insel Borkum - ein deutlich überdurchschnittliches Jahr.

Quelle: Umweltbundesamt

Die Gefahr durch Waldbrände kann reduziert werden, indem Gebiete mit besonders hohem Waldbrandrisiko frühzeitig identifiziert werden. Dann können entsprechende vorbereitende Maßnahmen (Präventionsmaßnahmen) getroffen werden.

In diesem interaktiven Arbeitsblatt soll ein Modell für die Vorhersage des Waldbrandrisikos in Deutschland entwickelt werden. Das Modell wird mit historischen Daten trainiert, um zu lernen, wann das Waldbrandrisiko besonders hoch ist.

Foto „Altkoenig Waldbrand 2023-06-12 16-43-23-SR“ (Ausschnitt) von Alexander Hoernigk unter der Lizenz CC BY 4.0 via Wikimedia Commons

2 Daten einlesen

Zunächst werden die (historischen) Daten eingelesen, die für die Erstellung des Vorhersagemodells benötigt werden.

Bei den Daten handelt es sich um verschiedene Klimadaten aus Deutschland, die von Satelliten gemessen wurden.

Die Daten beinhalten

die mittlere Oberflächentemperatur (engl. Land Surface Temperature) in Grad Celsius (°C)
den mittleren Vegetationsindex (NDVI). Dabei handelt es sich um einen Wert zwischen 0 und 1, welcher angibt, wie “gesund” die Vegetation ist. Je höher der Wert, desto stärker belaubt ist die Vegetation.
die mittlere kumulative Niederschlagsmenge (engl. Precipitation) in Millimeter (mm) und
die mittlere Anzahl der Waldbrände (engl. Active Fires) in Deutschland pro 1000 $m^{2}$ .

Die Daten decken den Zeitraum von Juni 2000 bis Juni 2023 ab.

Die Daten liegen jeweils als Mittelwert für einen Monat vor.

Daten einlesen

Start Over

Run Code

# Data Science Bibliothek importieren

import pandas as pd

# Daten einlesen

df = pd.read_csv(

'data/fire_prediction.csv',

index_col='time',

parse_dates=True

)

# Daten ausgeben

_pyodide_editor_2 = Object {code: null, options: Object, indicator: it}

Mit Hilfe der Funktion px.line() können die Daten in einem Liniendiagramm visualisiert werden.

Tipp

Durch Doppelklick auf eine der Variablen kann diese einzeln betrachtet werden. Dies ist hilfreich, um z.B. die NDVI-Kurve besser erkennen zu können.

Daten explorieren

Start Over

Run Code

# Bibliothek zum Erstellen von interaktiven Graphen

import plotly.express as px

# Daten in Liniendiagramm visualisieren

fig = px.line(df)

# Diagramm anzeigen

fig.show()

_pyodide_editor_3 = Object {code: null, options: Object, indicator: it}

3 Zusammenhänge erkennen und beschreiben

Zunächst soll untersucht werden, ob Zusammenhänge zwischen den verschiedenen Variablen vorliegen. Dazu werden die Variablen paarweise in einem Streudiagramm (scatter plot) gegenübergestellt.

3.1 Oberflächentemperatur (Land Surface Temperature)

Beginnen wir mit der Oberflächentemperatur. Auf der x-Achse ist die gemessene Oberflächentemperatur dargestellt. Auf der y-Achse ist die dazugehörige Anzahl der Waldbrände im gleichen Zeitraum dargestellt.

Streudiagramm

Start Over

Run Code

# Streudiagramm erzeugen

fig = px.scatter(

df,

x='land_surface_temp',

y='active_fires',

)

# Diagramm anzeigen

fig.show()

_pyodide_editor_4 = Object {code: null, options: Object, indicator: it}

Aufgabe 1

Betrachte das Streudiagramm.
Wie hängt die Oberflächentemperatur mit der Anzahl der Waldbrände zusammen?
Formuliere eine Gesetzmäßigkeit: “Je höher … , desto … .”

(5 Minuten)

Lösung

Aus der Darstellung ergibt sich folgender Zusammenhang:

Je höher die Oberflächentemperatur, desto höher die Anzahl der Waldbrände.

Der Zusammenhang is annähernd linear.

3.2 Niederschlag (Precipitation)

Betrachten wir nun die Niederschlagsmenge und wie diese sich auf die Waldbrandgefahr auswirkt.

Aufgabe 2

Erstelle ein Streudiagramm (Scatter Plot), welches die Niederschlagsmenge (precipitation) und die Anzahl der Waldbrände (active_fires) gegenüberstellt.
Orientiere dich dabei an dem vorherigen Beispiel für die Oberflächentemperatur.
Wie hängt die Niederschlagsmenge mit der Anzahl der Waldbrände zusammen?

(10 Minuten)

Aufgabe 2

Start Over Show Solution

Run Code

# Hier Programmcode einfügen

_pyodide_editor_5 = Object {code: null, options: Object, indicator: it}

Lösung

Um die Niederschlagsmenge mit der Anzahl der Waldbrände zu vergleichen, muss der Wert für den Parameter x durch den Spaltennamen für die Niederschlagsmenge ersetzt werden.

Aus der Darstellung ergibt sich der folgende Zusammenhang:

Je höher die Niederschlagsmenge, desto niedriger die Anzahl der Waldbrände.

# Programmcode mit Kommentaren
px.scatter(df, x='precipitation', y='active_fires', trendline='ols')

3.3 Vegetationsindex (NDVI)

Aufgabe 3

Erstelle ein Streudiagramm (scatter plot), welches den Vegetationsindex (ndvi) und die Anzahl der Waldbrände (active_fires) gegenüberstellt.
Wie hängt der Vegetationsindex mit der Anzahl der Waldbrände zusammen?

(10 Minuten)

Aufgabe 3

Start Over Show Solution

Run Code

# Hier Programmcode einfügen

_pyodide_editor_6 = Object {code: null, options: Object, indicator: it}

Lösung

Um den Vegetationsindex mit der Anzahl der Waldbrände zu vergleichen, muss lediglich der Parameter x durch den Spaltennamen des Vegetationsindex ersetzt werden.

Aus der Darstellung ergibt sich der folgende Zusammenhang:

Je höher der Vegetationsindex, desto höher die Waldbrandgefahr. Für sehr hohe Werte (gesunde Vegetation), nimmt die Waldbrandgefahr jedoch wieder ab. Daher besteht hier kein strikt linearer Zusammenhang.

px.scatter(
    df,
    x='ndvi',
    y='active_fires',
    trendline='ols' # Optional
)

3.4 Visualisierung in Form eines 3D-Streudiagramms

Um den Zusammenhang zwischen den Variablen besser zu verstehen, eignet sich zusätzlich die Darstellung in einem dreidimensionalen Scatterplot. Jede Achse repräsentiert eine der Variablen Oberflächentemperatur, Vegetationsindex und Niederschlagsmenge. Die Farbe der Punkte entspricht der Anzahl der Waldbrände.

Aus der Darstellung lässt sich ein Areal erkennen, in dem die Anzahl der Waldbrände besonders hoch ist.

Python Code

Start Over

Run Code

# 3D Streudiagramm

px.scatter_3d(

df,

x='ndvi',

y='precipitation',

z='land_surface_temp',

color='active_fires',

)

_pyodide_editor_7 = Object {code: null, options: Object, indicator: it}

4 Vorhersagemodell für die Waldbrandgefahr

Basierend auf den Erkenntnissen soll nun ein Vorhersagemodell für die Waldbrandgefahr entwickelt werden.

Stelle dir vor, du möchtest die aktuelle Waldbrandgefahr vorhersagen. Mit Hilfe von Satellitendaten kannst du die aktuelle Oberflächentemperatur, den Vegetationsindex und den Niederschlag ermitteln.

Um nun aus diesen Daten eine Vorhersage abzuleiten, wird ein (mathematisches) Modell benötigt. Dieses erhält die entsprechenden Daten als Eingabe und berechnet daraus die Anzahl der zu erwartenden Waldbrände (siehe Abb. 1).

Wir verwenden dafür ein sogenanntes Lineares Modell (auch Lineare Regression genannt). Das ist im Wesentlichen nichts anderes als eine lineare Funktion, die du bereits aus dem Mathematikunterricht kennen:

$y = f (x) = a \cdot x + b$

Wenn wir geeignete Parameter a und b bestimmt haben, können wir damit eine Vorhersage für die Anzahl der Waldbrände y aus unseren Eingabedaten x berechnen.

Da die Variable Anzahl der Waldbrände von den Variablen Oberflächentemperatur, Vegetationsindex und Niederschlag abhängt, wird diese auch abhängige Variable (oder Zielvariable) genannt und die anderen Variablen unabhängige Variablen (Eingabevariablen).

5 Einfache Lineare Regression

Wir betrachten zunächst nur die Oberflächentemperatur als abhängige Variable und lassen die Variablen Niederschlag und Vegetationsindex vorerst außen vor.

5.1 Modellannahme

Wir haben zu Beginn gesehen, dass die Anzahl der Waldbrände mit steigender Oberflächentemperatur zunimmt.

Wir nehmen daher an, dass ein linearer Zusammenhang (lineare Funktion) zwischen der Oberflächentemperatur und der Anzahl der Waldbände besteht. Diesen können wir mathematisch wie folgt ausdrücken:

$active_fires = a \cdot land_surface_temp + b$

$a$ (Steigung): Dieser Parameter zeigt, wie stark sich die Anzahl der Waldbrände ändert, wenn sich die Temperatur ändert. Ein positiver Wert von $a$ bedeutet, dass höhere Temperaturen zu mehr Waldbränden führen, während ein negativer Wert darauf hinweist, dass höhere Temperaturen zu weniger Waldbränden führen.
$b$ (y-Achsenabschnitt): Dieser Parameter gibt die Grundrate der Waldbrände an, wenn die Temperatur null ist. Man kann ihn als Ausgangspunkt oder Basiswert der Waldbrände sehen.

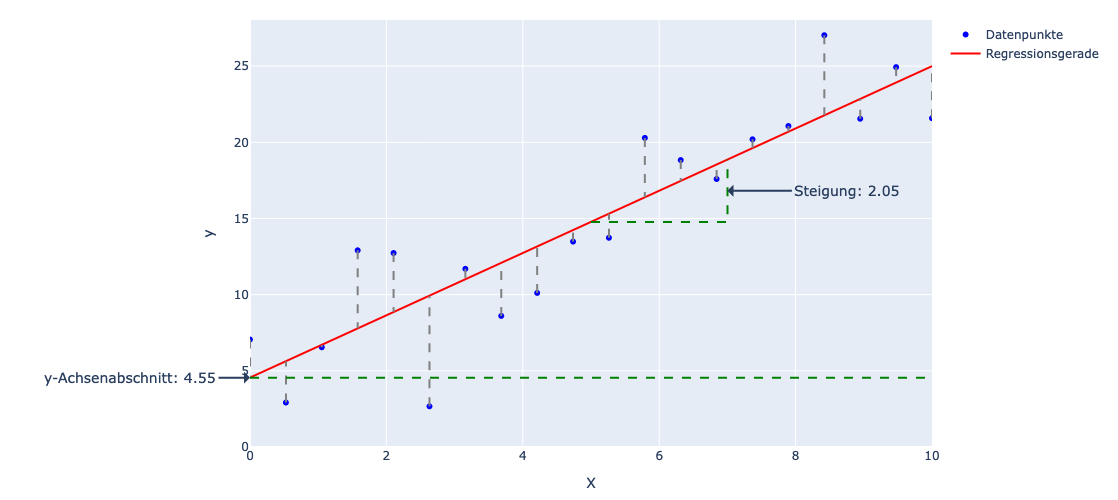
Das Ziel ist es, die Parameter a und b so zu bestimmen, dass die daraus resultierende lineare Funktion, die Daten “bestmöglich” beschreibt (siehe Grafik).

Zunächst erzeugen wir ein lineares Regressionsmodell. Dazu verwenden wir die Bibliothek sklearn, welche verschiedene Machine-Learning Modelle zur Verfügung stellt.

Python Code

Start Over

Run Code

# Bibliothek zum Modellieren von linearen Zusammenhängen

from sklearn.linear_model import LinearRegression

# Lineares Modell instanziieren

model = LinearRegression()

model

_pyodide_editor_8 = Object {code: null, options: Object, indicator: it}

5.2 Unabhängige und Abhängige Variablen festlegen

Nun definieren wir die unabhängige(n) Variable(n) (Eingabe) und die abhängige Variable (Ausgabe) wie oben beschrieben. In unserem Fall soll die Anzahl der Waldbrände anhand der Oberflächentemperatur vorhergesagt werden. Symbolisch ausgedrückt:

$land_surface_temp \to active_fires$

Daher ist die Variable Anzahl der Waldbände abhängig von der unabhängigen Variable Oberflächentemperatur.

Die abhängige Variable wird üblicherweise mit y bezeichnet. Die unabhängige Variable mit X.

Hinweis

Da es in der Regel mehr als eine unabhängige Variable gibt, wird ein großes X anstelle eines kleinen x verwendet. Die Variablen werden daher in einer Liste ['variable_1', 'variable_2', '...'] aufgelistet. In diesem Fall gibt es jedoch nur eine unabhängige Variable (land_surface_temp).

Python Code

Start Over

Run Code

# Liste der unabhängigen Variablen

X = df[['land_surface_temp']].values

# Abhängige Variable

y = df['active_fires'].values

# Anzeigen der ersten zehn Werte von X

print('X', X[:10])

# Anzeigen der ersten zehn Werte von y

print('y:', y[:10])

_pyodide_editor_9 = Object {code: null, options: Object, indicator: it}

6 Trainings- und Validierungsdaten

Bevor wir das Modell trainieren, teilen wir den Datensatz in zwei Teile auf: Trainingsdaten und Validierungsdaten. Die Trainingsdaten werden verwendet, um das Modell zu „lernen“, also die optimalen Parameter zu finden. Die Validierungsdaten dienen anschließend zur Bewertung, wie gut das Modell auf neue, bisher unbekannte Daten generalisiert.

Diese Aufteilung ist wichtig, um Überanpassung (Overfitting) zu vermeiden – das bedeutet, dass das Modell zwar die Trainingsdaten sehr gut vorhersagt, aber bei neuen Daten versagt.

Beispiel: Ein überangepasstes Modell könnte einfach die Zielwerte aus dem Training speichern und später bei gleichen Eingaben exakt wiedergeben. In den Trainingsdaten hätte es dann eine perfekte Vorhersage – aber sobald eine leicht andere Eingabe kommt (wie es bei echten Daten üblich ist), wäre die Vorhersage völlig unbrauchbar. Durch Validierungsdaten können wir prüfen, ob das Modell wirklich Zusammenhänge gelernt hat, oder nur auswendig gelernt hat.

Python Code

Start Over

Run Code

# Importiere Funktion für die Aufteilung der Daten in Trainings- und Validierungsdaten

from sklearn.model_selection import train_test_split

# Daten in Trainings- und Validierungsdaten aufteilen

X_train, X_test, y_train, y_test = train_test_split(

test_size=0.25, # Anteil der Testdaten (25 Prozent)

random_state=42 # Stellt sicher, dass die "zuffälige" Auswahl immer gleich ausfällt

)

print(f'Anzahl der Traningsdaten:', len(X_train))

print('Anzahl der Validierungsdaten:', len(X_test))

_pyodide_editor_10 = Object {code: null, options: Object, indicator: it}

Der Parameter random_state=42 sorgt dafür, dass die “zufällige” Aufteilung der Daten bei jeder Ausführung gleich ist. Das ist wichtig, damit wir bei der Modellentwicklung und Evaluation stets mit denselben Trainings- und Validierungsdaten arbeiten und vergleichbare Ergebnisse erhalten.

6.1 Modell trainieren

Wie bereits erwähnt, müssen wir nun die Parameter a und b so bestimmen, dass die daraus resultierende lineare Funktion möglichst gut an die Daten angepasst ist (engl. fit). Um die Güte der Anpassung messen zu können, benötigen wir ein sogenanntes Fehlermaß. In unserem Fall wählen wir die mittlere quadratische Abweichung (engl. Mean Squared Error).

Vereinfacht gesagt: Je weiter die Punkte im Mittel von der Geraden entfernt sind, desto höher ist der Mean Squared Error. Das Ziel ist es daher, den Mean Squared Error zu minimieren. Es handelt sich daher um ein sogenanntes Optimierungsproblem.

Aufgabe 4

Optimale Parameter bestimmen

Verändere die Schieberegler für die Steigung und den y-Achsenabschnitt so, dass der Mean Squared Error minimal wird.
Lese anschließend die beiden Parameter a und b ab.

(5 Minuten)

viewof slope = Inputs.range([-0.5, 1.5], {step: 0.01, label: "Steigung (a)"})
// slider returning intercept value
viewof intercept = Inputs.range([-5, 30], {step: 0.1, label: "Y-Achsenabschnitt (b)"})

slope = 0.5

intercept = 12.5

Lösung

Die optimale Belegung der Parameter ist:

a = 0.48
b = 3.50
mse = 14.7

6.2 Gradientenverfahren

Das manuelle Anpassen der Parameter ist zeitaufwändig und unpräzise. Unser Modell verwendet zwar nur zwei Parameter, a und b, in komplexeren Modellen können jedoch weit mehr Parameter erforderlich sein.

Anstatt die Parameter manuell einzustellen, lernt unser Modell automatisch Schritt für Schritt die optimale Parameterkonfiguration aus den Daten. Dieser Prozess wird als maschinelles Lernen bezeichnet. Die Umsetzung variiert je nach verwendetem Lernverfahren, das Grundprinzip bleibt jedoch immer gleich.

Um das Modell zu trainieren, nutzen wir die Methode fit(X, y), wobei X die Eingabedaten und y die zugehörigen Zielwerte sind. Diese Methode passt die Parameter a und b automatisch an, um die optimale Konfiguration zu finden.

Hinweis

Wir gehen an diesere Stelle nicht im Detail auf die zugrundeliegende Funktionsweise das Gradientenverfahrens ein. Die Idee dahinter ist den Wert der Ableitung (Gradient) der Fehlerfunktion (Mean-Squared-Error) für die jeweilige Paramterkombination zu bestimmen. Der Gradient zeigt dann an, in welche “Richtung” die Paramter angepasst werden müssen, um den Wert der Fehlerfunktiont zu reduzieren. Dieser Schritt wird solange wiederholt, bis keine nennenswerte Verbesserung mehr feststellbar ist.

Python Code

Start Over

Run Code

# Passe die Paramter des Modells and die Traningsdaten an

model.fit(X_train, y_train)

_pyodide_editor_12 = Object {code: null, options: Object, indicator: it}

Die folgende Animation zeigt die schrittweise Anpassung der Parameter.

6.3 Parameter ermitteln

Nachdem das Modell an die Daten angepasst wurde, können wir die Parameter a und b auslesen.

Python Code

Start Over

Run Code

# Steigung (Regressionskoeffizient)

a = model.coef_[0]

# y-Achstenabschnitt

b = model.intercept_

print('Steigung:', a.round(4))

print('y-Achsenabschnitt:', b.round(4))

_pyodide_editor_13 = Object {code: null, options: Object, indicator: it}

Aufgabe 5

Angenommen es wurden 15 Grad Celsius Oberflächentemperatur gemessen.
Berechnen Sie mit Hilfe der ermittelten Steigung und des y-Achsenabschnitts die zu erwartende Anzahl an Waldbränden.

(5 Minuten)

Aufgabe 5

Start Over Show Solution

Run Code

# Hier Programmcode einfügen

_pyodide_editor_14 = Object {code: null, options: Object, indicator: it}

Lösung

Die Anzahl der zu erwartenden Waldbrände ergibt sich aus der Funktion $f$ :

$f (x) = a \cdot x + b$

Um die Anzahl der zu erwartenden Waldbrände vorherzusagen, muss nun für x der Wert 15 eingesetzt werden.

$f (15) = a \cdot 15 + b$

a * 15 + b

np.float64(10.725801453435622)

6.4 Vorhersage machen

Anschließend können wir mit Hilfe des trainierten Modells eine Vorhersage treffen.

Dazu verwenden wir die Methode predict(). Diese erwartet eine oder mehrere Eingaben im gleichen Format wie die Trainingsdaten – das heißt, mit derselben Anzahl und Reihenfolge der Variablen. Als Ausgabe erhalten wir eine Vorhersage für die Zielgröße, in diesem Fall die zu erwartende Anzahl an Waldbränden.

Beispiel: Angenommen es wurden 32 Grad Oberflächentemperatur gemessen. Unser Modell liefert folgende Anzahl zu erwartender Waldbrände:

Python Code

Start Over

Run Code

# Vorhersage für 32 Grad Oberflaechentemperatur

model.predict([[32]])

_pyodide_editor_15 = Object {code: null, options: Object, indicator: it}

Um unser Modell im Anschluss zu evaluieren, erstellen wir eine Vorhersage für die Validierungsdaten df_val. Dann vergleichen wir die vorhergesagten Werte mit den tatsächlichen Beobachtungen, um zu beurteilen, wie gut das Modell generalisiert.

Python Code

Start Over

Run Code

# Vorhersage erstellen

y_pred = model.predict(X_test)

# Vorhersage anzeigen (erste 10 Werte)

y_pred[:10]

_pyodide_editor_16 = Object {code: null, options: Object, indicator: it}

Hinweis

Das Modell erwartet als Eingabe immer eine Liste von Messungen. Jede Messung besteht wiederum aus einer Liste von Messwerten (ein Messwert für jede unabhängige Variable). Daraus ergibt sich die Schreibweise mit doppelten Klammern [[32]].

6.5 Modell evaluieren

Um das Modell zu evaluieren, vergleichen wir die Vorhersagen des Modells mit den tatsächlich gemessenen Werten.

Dazu erstellen wir ein Streudiagramm. Auf der y-Achse werden die tatsächlich gemessenen Werte dargestellt, während die x-Achse die vorhergesagten Werte zeigt.

Eine gute Vorhersage bedeutet, dass die vorhergesagten Werte den tatsächlichen Werten weitgehend entsprechen. Das heißt, die x- und y-Koordinaten eines Punktes sind nahezu identisch, und der Punkt liegt nahe an der Geraden $f (x) = x$ . Befinden sich die Punkte jedoch weit entfernt von dieser Geraden, deutet das darauf hin, dass das Vorhersagemodell die Daten nicht zuverlässig abbildet.

Hinweis

Die Gerade wird auch Identitätsgerade genannt.

Python Code

Start Over

Run Code

from sklearn.metrics import PredictionErrorDisplay

ped = PredictionErrorDisplay(y_true=y_test, y_pred=y_pred)

display = ped.plot(kind="actual_vs_predicted")

_pyodide_editor_17 = Object {code: null, options: Object, indicator: it}

Mit der Methode score(X, y) lässt sich ein Maß für die Güte des Modells bestimmen. Dabei handelt es sich um das sogenannte Bestimmtheitsmaß $R^{2}$ , welches angibt, wie gut das Modell die Daten beschreibt.

Ein Wert von 1 würde bedeuten, dass das Modell die Daten perfekt beschreibt, d.h. dass alle Punkte genau auf der Geraden liegen. Ein Wert von 0 bedeutet, dass kein linearer Zusammenhang besteht.

Es gilt: Je höher der Score, desto besser beschreibt das Modell die zugrunde liegenden Daten.

Formel

Das Bestimmtheitsmaß (R^2) wird definiert als

$R^{2} = 1 - \frac{\sum_{i = 1}^{n} (y_{i} - {\hat{y}}_{i})^{2}}{\sum_{i = 1}^{n} (y_{i} - \bar{y})^{2}}$

wobei
- $y_{i}$ = beobachtete Werte,
- ${\hat{y}}_{i}$ = durch das Modell vorhergesagte Werte,
- $\bar{y}$ = Mittelwert der beobachteten Werte,
- $n$ = Anzahl der Beobachtungen.

Modell evaluieren

Start Over

Run Code

# Bestimmtheitsmaß berechnen

r2 = model.score(X_test, y_test)

_pyodide_editor_18 = Object {code: null, options: Object, indicator: it}

Der ermittelte Wert deutet darauf hin, dass zwar ein linearer Zusammenhang besteht, dieser jedoch nicht ausreicht, um die Komplexität der Daten vollständig zu erfassen. Das Modell erklärt also nur einen Teil der Variabilität in den Beobachtungen.

Um die Vorhersagegenauigkeit zu verbessern, erweitern wir im nächsten Teil das lineare Modell um zusätzliche Eingabevariablen.

7 Zusammenfassung

In diesem Notebook hast du gelernt, wie du:

Daten aus einer CSV-Datei mit read_csv() einlesen und in einem DataFrame speichern kannst,
die Daten explorierst und mit Diagrammen wie px.line() (Liniendiagramm) und px.scatter() (Streudiagramm) visualisierst,
die Beziehung zwischen zwei Variablen – hier Oberflächentemperatur und Anzahl aktiver Brände – untersuchst,
ein einfaches lineares Regressionsmodell mit LinearRegression() aus sklearn aufbaust,
das Modell trainierst (fit) und Vorhersagen machst (predict),
die Modellgüte mit Metriken wie dem Bestimmtheitsmaß (R²) einschätzt,
den Einfluss der Oberflächentemperatur auf die Waldbrandgefahr interpretierst.

Downloading resource: fire_prediction.csv

Wiederverwendung

CC BY-SA 4.0

Zitat

Mit BibTeX zitieren:

@online{sparmann2025,
  author = {Sparmann, Sören},
  title = {Einfache Lineare Regression (Teil 1)},
  date = {2025-09-14},
  url = {https://material.cdec.io/modul_2/submodules/02_waldbrand/01_einfache_lineare_regression.html},
  langid = {de}
}

Bitte zitieren Sie diese Arbeit als:

Sparmann, Sören. 2025. “Einfache Lineare Regression (Teil 1).” September 14, 2025. https://material.cdec.io/modul_2/submodules/02_waldbrand/01_einfache_lineare_regression.html.